
发表日期: 2021-09-14 17:44:06 浏览次数:108
保定网站建设_保定网站设计_保定百度排名_保定网络公司_保定网页设计-保定百度推广

保定,古称上谷、保州、保府,因城池似靴,又名靴城,位于河北省中心地带、太行山东麓,是京津冀地区中心城市,中国(河北)自由贸易试验区组成部分。 [102]
保定与北京相伴而生,保定之名取自“保卫大都,安定天下”。保定与北京、天津构成黄金三角,自古是“北控三关,南达九省,地连四部,雄冠中州”的通衢之地,历来为京畿重地和“首都南大门”。清代,保定为直隶省省会,是直隶总督驻地,自1669年至1968年三百年间,为河北政治、经济、文化、军事中心以及区域性政治中心,新中国成立后也两度为河北省省会。 [106]
保定是尧帝的故乡,有三千多年建城史,为燕国、中山国、后燕立都之地;诞生了荆轲、刘备、赵匡胤等一批历史名人;市内文物古迹众多,如古莲花池、大慈阁、直隶总督署、清西陵等。
保定是国家历史文化名城、中国优秀旅游城市、国家园林城市,是中国首个创新驱动发展示范市、全国双拥模范城,也是戏曲之乡、游泳之乡、“长寿之城”,因体育冠军辈出,又称“冠军之城”。2017年,保定市入选“2017年度中国最具投资潜力城市50强”。 [1-10]
截至2020年9月,保定市辖5区、4市、15县,总面积22135平方公里,另设1个国家级高新区、1个副地级白沟新城。 [11] 拥有河北大学、华北电力大学、河北农业大学、中央司法警官学院等18所高校。 [12-15] [103]
2017年4月,中共中央、国务院决定设立河北雄安新区,涉及保定市雄县、容城县、安新县。雄安新区是继深圳经济特区和上海浦东新区后又一具有全国意义的新区。
输出结果为:
数组 a:[[1 2] [3 4]]数组 b:[[11 12] [13 14]]内积:[[35 41] [81 95]]数组 a:[[1 2] [3 4]]数组 b:[[11 12] [13 14]]内积:[[35 41] [81 95]]
内积计算式为:
1*11+2*12, 1*13+2*14 3*11+4*12, 3*13+4*14
numpy.matmul 函数返回两个数组的矩阵乘积。 虽然它返回二维数组的正常乘积,但如果任一参数的维数大于2,则将其视为存在于最后两个索引的矩阵的栈,并进行相应广播。
另一方面,如果任一参数是一维数组,则通过在其维度上附加 1 来将其提升为矩阵,并在乘法之后被去除。
对于二维数组,它就是矩阵乘法:
输出结果为:
[[4 1] [2 2]]
二维和一维运算:
输出结果为:
[1 2] [1 2]
维度大于二的数组 :
输出结果为:
[[[ 2 3] [ 6 11]] [[10 19] [14 27]]]
numpy.linalg.det() 函数计算输入矩阵的行列式。
行列式在线性代数中是非常有用的值。 它从方阵的对角元素计算。 对于 2×2 矩阵,它是左上和右下元素的乘积与其他两个的乘积的差。
换句话说,对于矩阵[[a,b],[c,d]],行列式计算为 ad-bc。 较大的方阵被认为是 2×2 矩阵的组合。
输出结果为:
-2.0
输出结果为:
[[ 6 1 1] [ 4 -2 5] [ 2 8 7]]-306.0-306
numpy.linalg.solve() 函数给出了矩阵形式的线性方程的解。
考虑以下线性方程:
x + y + z = 62y + 5z = -42x + 5y - z = 27
可以使用矩阵表示为:
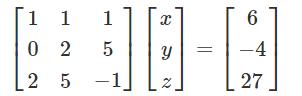
如果矩阵成为A、X和B,方程变为:
AX = B或X = A^(-1)B
numpy.linalg.inv() 函数计算矩阵的乘法逆矩阵。
逆矩阵(inverse matrix):设A是数域上的一个n阶矩阵,若在相同数域上存在另一个n阶矩阵B,使得: AB=BA=E ,则我们称B是A的逆矩阵,而A则被称为可逆矩阵。注:E为单位矩阵。
输出结果为:
[[1 2] [3 4]][[-2. 1. ] [ 1.5 -0.5]][[1.0000000e+00 0.0000000e+00] [8.8817842e-16 1.0000000e+00]]
现在创建一个矩阵A的逆矩阵:
输出结果为:
数组 a:[[ 1 1 1] [ 0 2 5] [ 2 5 -1]]a 的逆:[[ 1.28571429 -0.28571429 -0.14285714] [-0.47619048 0.14285714 0.23809524] [ 0.19047619 0.14285714 -0.0952381 ]]矩阵 b:[[ 6] [-4] [27]]计算:A^(-1)B:[[ 5.] [ 3.] [-2.]]
结果也可以使用以下函数获取:
x = np.dot(ainv,b)
保定网站建设_保定网站设计_保定百度排名_保定网络公司_保定网页设计-保定百度推广


 服务热线
服务热线
 顶部
顶部
备案号: 苏ICP备11067224号
CopyRight © 2011 书生商友信息科技 All Right Reserved
24小时服务热线:400-111-6878 E-MAIL:1120768800@qq.com QQ:1120768800
网址: https://www.768800.com 网站建设:上往建站
关键词: 网站建设| 域名邮箱| 服务器空间| 网站推广| 上往建站| 网站制作| 网站设计| 域名注册| 网络营销| 网站维护|
企业邮箱| 虚拟主机| 网络建站| 网站服务| 网页设计| 网店美工设计| 网站定制| 企业建站| 网站设计制作| 网页制作公司|
400电话办理| 书生商友软件| 葬花网| 调温纤维| 海洋馆运营维护| 北京保安公司| 殡仪馆服务| 殡葬服务| 昌平殡葬| 朝阳殡葬|
欢迎您免费咨询,请填写以下信息,我们收到后会尽快与您联系
服务热线:400-111-6878